

General overview


-
Axis 1: Anomalous Elasticity in the Ordered Phases of Crystalline Membranes
Topic 1: Stability of the flat phase
The stability of bidimensional crystals such as graphene, phosphorene, MoS2, ... appears to be quite paradoxical. Indeed, it is expected from Mermin and Wagner's theorem that such an ordered phase cannot be stable in two dimensions for any non zero temperature. As it turns out, a detailed study of the symmetries of the problem and the associated Goldstone theorem shows that crystalline membrane possess two distinct massless modes in strong interaction with each other: the acoustic phonons, as in usual crystals, and the flexurons which are the vibrations in the direction(s) perpendicular to the membrane's ground state. Thus, the phonons carry an effective interaction between flexurons which is long-range due to their massless character and the Mermin-Wagner theorem does not apply, thereby explaining the stability of such systems.
Associated publication: [1] Spontaneous symmetry breaking and the flat phase of crystalline membranes, O Coquand - Physical Review B, (2019)



Topic 2: The buckling transition
When submitted to an external source of stress, crystalline membranes can react in three different ways: (i) deform, (ii) buckle, (iii) overstretch.
This behaviour is related to a phase transition, called the buckling transition, which is of second order, with a well-identified critical point and associated universal critical exponents that can be, at least in principle, compared with experiments.
The use of non-perturbative renormalisation group allowed us to confirm the extrapolated perturbative scenario, as well as highlighting how some fundamental symmetries of the system constrain strongly the possible evolutions, thereby explaining the success of perturbative approaches to the renormalisation group on this problem. Finally, we were able to reconstruct the full phase diagram of membranes in the (stress, size, Temperature) space,which is the analogous of the (P,V,T) space used in the usual study of pure substances.
Associated publications: [1] O. Coquand and D. Mouhanna, to be published

Topic 3: Effect of quantum fluctuations
The question of the stability of crystalline membranes with respect to quantum fluctuations, that dominate over the thermal ones at low temperature, was a subject of controversy. The use of a non-perturbative renormalisation group approximation scheme tailored precisely for this problem allowed us not only to show their stability at low temperatures, but also to study the influence of quantum and thermal fluctuations on their elasticity at any intermediate temperature. In addition, we clarified the existing debate about the question of the minimum temperature from which quantum effects begin to become visible.
Associated publications: [1] Flat phase of quantum polymerized membranes, O Coquand, D Mouhanna - Physical Review E, (2016)
[2] O. Coquand and D. Mouhanna, to be published
Topic 4: Thermodynamics of disordered membranes


Materials are never perfect down to the microscopic scale: there are always defects such as atom vacancies, anomalies in the local connectivity, inclusion of alien atoms, ... This project was centered on the effect on the elasticity of crystalline membranes of such defects. After showing that no non-trivial effect was present if the impurities thermalise with the membrane, we concentrated on the case of frozen disorder where the impurities can be treated as static at the scale of the membrane's dynamical evolution. Importantly, we discovered a new phase transition, absent from the previous perturbative studies, that is supported by experimental evidence, between the flat phase of pure membranes to a wrinkled phase at high density of defects and/or low temperature. This phase is also flat on average, but with a different roughness exponent. Quantitative comparison of the (universal) roughness exponents predicted in the wrinkling transition gives further support to our work when compared to experiment.Thanks to the non-perturbative character of our approach, we were also able to take the perturbative limit and explain why the wrinkling transition was absent from previous studies: close to 4 dimensions, the wrinkled phase fixed point and the critical fixed point associated to the phase transition collapse onto each other, so that at least two loops are required in the perturbative series to be able to observe such behaviour.Using this convincing characterisation of the (ordered) wrinkled phase, we computed its thermodynamic characteristics.
Associated publications: [1] Glassy phase in quenched disordered crystalline membranes, O Coquand, K Essafi, JP Kownacki, D Mouhanna - Physical Review E, (2018)
[2] Universal behaviors in the wrinkling transition of disordered membranes, O Coquand, K Essafi, JP Kownacki, D Mouhanna - Physical Review E, (2020)
[3]Wrinkling transition in quenched disordered membranes at two loops, O Coquand, D Mouhanna - Physical Review E, (2021)[4] O. Coquand and D. Mouhanna, to be published
-
Axis 2: The Internal Structure of Liquids
Topic 1: Analytical Structure Factor of Square-shoulder Systems


The square-shoulder potential, combination of a hard-sphere potential with a finite region of constant, positive, potential, is an interesting toy-model from several perspectives: (i) the behaviour of systems with a combination of a hard and a soft core is believed to be largely universal, (ii) it possesses two limits (the high temperature and low temperature ones) in which the effective behaviour of the particles is that of a hard sphere system. Hence, when constructing an analytical estimate of the structure factor of such a system, there are two well-controlled limits. Together with M. Sperl, we thus built the structure factor of the square-shoulder system both in a low temperature and in a high temperature expansions around the known hard sphere solution of Wertheim and Baxter. What our work revealed is that, already at this order the high temperature expansion is ill-behaved from a number of perspectives, thereby hindering the possibility of accessing the system by a perturbative expansion in this limit. Following another route (the Rational Fraction Approximation), we nevertheless showed that it is possible to build a fully analytical estimate of the structure factor of the square-shoulder, and to make it match the best known equations of state of the hard spheres system in the low and high temperature limits. Getting a fully analytical formula for the structure factor, in addition to revealing facts about the physical behaviour of the system, allows to significantly speed-up the computations based on approaches like the mode-coupling approximation that rely heavily on having good estimates of the structure factor at any packing fraction and wave-vector.
Associated publications: [1] Temperature expansions in the square-shoulder fluid. I. The Wiener–Hopf function, O Coquand, M Sperl - The Journal of Chemical Physics, (2020)
[2] Temperature expansions in the square-shoulder fluid. II. Thermodynamics, O Coquand, M Sperl - The Journal of Chemical Physics, (2020)
[3] O. Coquand and M. Sperl, to be published
Topic 2: The inverse problem in dense systems



The inverse problem consists in reconstructing an effective pair interaction potential from structural data. Although a number of techniques are already available, they are generally very slow because at each step of the algorithm, a new guess potential is generated, and a full simulation of the system has to be realised to compare the results obtained with the guessed potential to the initial dataset. In this work, we restrain ourselves to develop a method allowing to skip this simulation step, thereby greatly enhancing the speed of the inversion algorithm, and opening the possibility to realise a much greater number of steps, and thus to get more precise results within a very reasonable computation time. Another constraint we put on our method is for it to be able to describe with a high degree of precision dense systems, that is liquids and not only gases. Our algorithm revealed to be particularly robust, being able to reconstruct potentials from simulated data not only on usual liquid potentials (Lennard-Jones, Yukawa, Morse), but also on shoulder potentials having a second length scale that appears to be very well resolved, on long range potentials, and on glass former potentials (like the Dzugutov potential) even for high densities, which is quite remarkable in regard of what current inversion algorithms are able to do.
Associated publications: [1] O. Coquand, D. Paolino and L. Berthier, to be published
-
Axis 3: The Rheology of Granular Liquids
Topic 1: Rheology of Granular Liquids from first principles

By importing tools used from the study of the slow-down of the dynamics in supercooled liquids the group of Matthias Sperl that I integrated in 2018 was able to develop the first theoretical model able to capture the physics of granular liquid flows. However, this model is based on the Mode-coupling equations, derived from the formalism of Mori and Zwanzig, which makes the equation of motion an integro-differential equation including a convolution with a non-trivial kernel. This equation can only be solved numerically, even in basic models. Therefore, I developed a series of toy-models that enable to capture the physics at play in terms of the fundamental processes at play at the different scales: collisions (microscopic), cage-effect, or collectiveblocking effect (mesoscopic), and particle advection (macroscopic).


These toy-models loose the quantitative predictive power of the original model, but provide a clear picture of the physics at play in the system, which has been validated by the comparison with experimental results, as well as the study of its prediction in the dilute, gaseous, limit (see below).The quality of the comparison of this approach with the existing experimental literature further allowed to make simple and easily testable laws for the rheology of granular suspensions, granular fluids outside of the Bagnold flow regime, as well as concrete geophysical models.

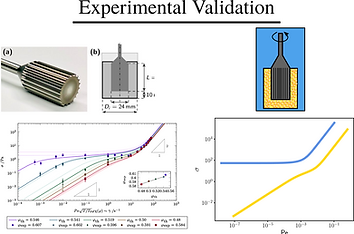
Associated publications: [1] Integration through transients approach to the mu(I) rheology, O Coquand, M Sperl, T Kranz - Physical Review E, (2020)
[2] Rheology of granular liquids in extensional flows: Beyond the mu(I)-law, O Coquand, M Sperl - Physical Review E, (2021)[3] Understanding dense granular flow from first principles, WT Kranz, O Coquand, O D'angelo - Science Talks, (2022)[4] Granular rheology: A tale of three time scales, O Coquand, WT Kranz, M Sperl - Physical Review E, (2025)
Topic 2: Dynamical yield criterion in granular matter

The results derived for the deformation of granular liquids can be extrapolated in the limit of zero shear rate, thereby giving access to the so-called dynamical yield surface of the material (it is dynamical in the sense that aging effects are not accessible through this procedure, which gives instead access to what is called the critical state in soil mechanics, that is the properties that the material reaches in the limit where it is deformed many times, which converge to a finite value). The use of the toy-models allows to express the form of the yield surface analytically, which reveals peculiar and interesting behaviour: at low pressures, the shape of the yield surface is that of a Drucker-Prager solid, corresponding to the fracture ;ode of soft materials; at high pressures on the other hand, the shape of the yield surface closely resembles that of a Ladé-Duncan, or Matsukoa-Nakai material, characteristic of the rupture of sedimentary rocks.
Associated publications: [1] Dynamical yield criterion for granular matter from first principles, O Coquand, M Sperl - Physical Review E, (2024)
Topic 3: The Liquid-Gas Transition in Granular systems

For more than twenty years, it has been an established fact in the experimental literature that granular matter presents two distinct fluid states: a gas state at low density, and a liquid state with a significantly different rheology. However, the mechanism at the origin of this liquid-gas transition is still elusive in such a system that does not present any form of attractive interaction, and that is intrinsically out of equilibrium, granular particles being dissipative by nature.I recently proposed a model to identify precisely the location of the liquid-gas transition in granular systems, using the toy-models initially derived to understand the liquid state to analyse the underlying physical mechanisms governing the transition. This model is substantiated by exhaustive comparison with the models of the Revised Enskog Theory class used to describe the gaseous state. As a byproduct, it also allows to understand why such models fail to capture the physics of the liquid state. The main predictions of this work are experimentally testable with our current level of technology.
Associated publications: [1] The liquid-gas transition in granular matter: A question of effective friction?, O Coquand - Journal of Rheology, (2025)
-
Axis 4: Scale-dependent Energy Transfers in Driven-Dissipative Systems
Topic 1: Energy cascades in driven Granular systems

When comparing the balance of energy in a sheared granular system to that of a turbulent Newtonian liquid, it is striking to see how much these problems are qualitatively similar: at a macroscopic scale, energy is injected into the system through a forcing mechanism, energy is then transported across the flow from the large scales structures to smaller and smaller ones until it is finally dissipated ate the microscopic scale. The main difference between the two systems, at least in the Bagnold flow regime of granular liquids, is the microscopic dissipation mechanism: momentum transfer between small scale vortices in one case, particle's collisions in the other.
It becomes then natural to wonder how far does the analogy go. In particular, does the granular cascade belong to the same universality class as that predicted by Kolmogorov in Newtonian liquids? Some recent numerical results seem to indicate a new type of universal behaviour, but they are very scarce (only one study in 3D to the best of my knowledge), and the proximity between the universal exponents in both cases further indicate that extra care is needed before concliding.
Associated publications: [1] Energy Cascades in Driven Granular Liquids: A new Universality Class? I: Model and Symmetries, O Coquand - arXiv:2504.12166, (2025)
Topic 2: Universality class(es) in compressible turbulence

The question of the scaling of the energy power spectrum in incompressible fluids has been settled by Kolmogorov in 1941. The question of compressible fluids on the other hand is still largely mysterious to our days. In particular, different numerical studies under different conditions have yielded different results, rendering a blurry picture of the problem.
By examining carefully the symmetries of the action associated to the compressible Navier-Stokes equation, I showed that, contrary to what is often assumed, the longitudinal velocity mode belongs to the 3D-Burgers class of fields, and not to the 1D-Burgers one (it has one direction of polarisation but still acts on a three dimensional space). This difference is crucial since the associated renormalisation group flow diagram presents two stable scaling behaviours at large scales: the Edwards-Wilkinson (EW) one, and the Kardar-Parisi-Zhang (KPZ) one, contrary to the one dimensional Burgers case where only the KPZ fixed point is stable in the infrared limit. This simple change of nature of the field could thus alone explain the dispersion of the results in the current literature. This work needs to be refined and is largely still in progress.
Associated publications: [1] The power spectrum of compressible turbulence: A story in symmetries, O Coquand - Symmetry 17(12) 2044 (2025)
